12.9 Log-Log Models
Using natural logs for variables on both sides of your econometric specification is called a log-log model. For example, consider a demand curve with constant elasticity:
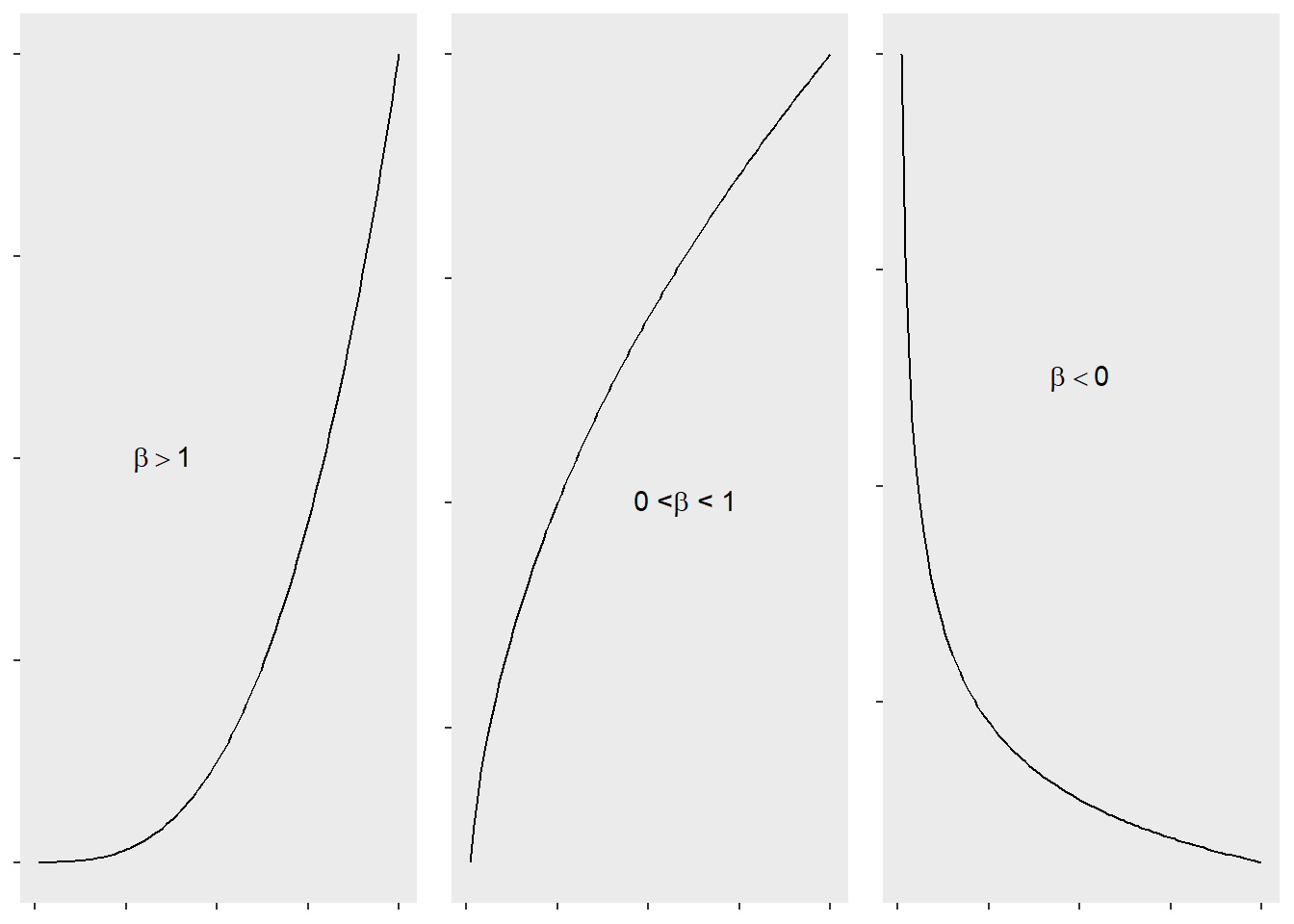
\[Q=\alpha P^\beta\] where \(Q\) is the demand, \(\alpha\) is a shifting parameter, \(P\) is the price , and \(\beta\) is less than zero for a downward-sloping demand curve.
If we take the natural log of both sides, we obtain:
\[\log Q= \log \alpha + \beta \log P\] that can be treated as a linear regression model.
If your model is not linear in parameters, sometimes a log transformation achieves linearity.
In general, if we have
\[Y_i=\alpha X_i^\beta\] We can use OLS to fit
\[\log Y_i= \log \alpha + \beta \log X_i\] where \(\log \alpha\) in the intercept of the straight line.
The coefficients in a log-log model represent the elasticity of the \(Y\) variable with respect to the \(X\) variable.
In other words, the coefficient is the estimated percent change in the dependent variable for a percent change in the independent variable.
References: